Next Permutation

Description

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.

If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).

The replacement must be in-place and use only constant extra memory.

Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.

1,2,3 → 1,3,2 3,2,1 → 1,2,3 1,1,5 → 1,5,1

实现字典序排列的 nextPermutation 方法，假如已经是最大排列，则输出最小排列。

字典序排列

我们在字符串大小比较时，就已经使用了字典序:

例如：abc < abcd < abde < afab

所以字典序排列算法中有：

  • 最小排列：1-n，eg：1,2,3,4
  • 最大排列：n-1，eg：4,3,2,1
  • next-permutation：根据当前排列，生成恰好比它大的下一个排列

通过字典序树可以更好的理解： 字典序树

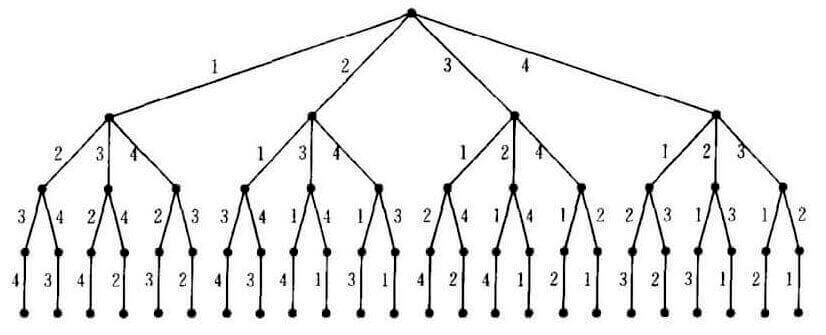
Solution

参考 wikipedia 中关于字典序排列的算法描述：

  1. Find the largest index k such that a[k] < a[k + 1]. If no such index exists, the permutation is the last permutation.
  2. Find the largest index l greater than k such that a[k] < a[l].
  3. Swap the value of a[k] with that of a[l].
  4. Reverse the sequence from a[k + 1] up to and including the final element a[n].

假设当前排列为长度为n+1的数组a，则其下一个排列的算法为:

  1. 查找最大的索引k，满足a[k] < a[k + 1]。如果不存在则当前已经是最大排列。
  2. 查找最大索引l，满足l > k && a[k] < a[l]。
  3. 交换a[k]和a[l]
  4. 将a[k + 1], a[k + 2], ..., a[n]倒序

实现代码如下： 

func nextPermutation(nums []int) {
    length := len(nums)
    if length == 1 {
        return
    }

    k := length - 2
    for ; k >= 0; k-- {
        if nums[k] < nums[k+1] {
            break
        }
    }

    if k == -1 {
        // 当前已经是最大排列，则输出最小排列
        reverse(nums)
        return
    }

    l := length - 1
    for ; l > k; l-- {
        if nums[l] > nums[k] {
            break
        }
    }

    // 交换 a[k] 和 a[l]
    swap(nums, k, l)

    // 倒序 a[k]...a[n]
    reverse(nums[k+1:])
}

// 交换两个数
func swap(nums []int, i, j int) {
    tmp := nums[i]
    nums[i] = nums[j]
    nums[j] = tmp
}

// 将slice倒序
func reverse(nums []int) {
    length := len(nums)
    for i := 0; i < length / 2; i++ {
        swap(nums, i, length - i - 1)
    }
}

Similar Problem