Description

Unique Paths

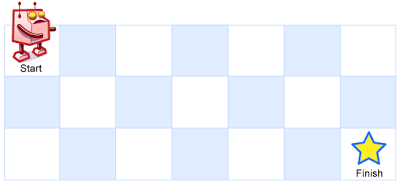
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

在m x n的方格中，从左上角走到右下角的不同路径有几种？（只允许向右和向下走）

Solution

这道题目可以转换为数学题：

m x n的方格要从左上角走到右下角，需要经过m - 1次Right和n - 1次Down操作。 所以总共是m + n - 2次操作，而操作顺序的不同，则对应路径不同。

这就转换成了数学的排列问题：C(m + n -2, n - 1)。 在m + n - 2操作中取Down操作的位置，其余位置就是Right操作。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

func uniquePaths(m int, n int) int {
    total := (m + n - 2)
    option := n - 1

    // C(3, 1) 与 C(3, 2)相等
    if m-1 < option {
        option = m - 1
    }

    if option <= 0 {
        return 1
    }

    // 计算C(m + n - 2, option)
    pp, qq := 1, 1
    for i := 1; i <= option; i++ {
        pp *= total
        qq *= i
        total--
    }

    return pp / qq
}

Similar Problem