Description
Minimum Window Substring
Given a string S and a string T, find the minimum window in S which will contain all the characters in T in complexity O(n).
Example:
Input: S = "ADOBECODEBANC", T = "ABC"
Output: "BANC"
Note:
- If there is no such window in S that covers all characters in T, return the empty string “”.
- If there is such window, you are guaranteed that there will always be only one unique minimum window in S.
给出两个字符串S和T,在S中找到一个最短的子串,它包含T中所有的字符。
需要注意的是的是T中一个字符会出现多次,在子串同样需要多次。
Solution
-
设两个指针表示子串的首尾:left,right:
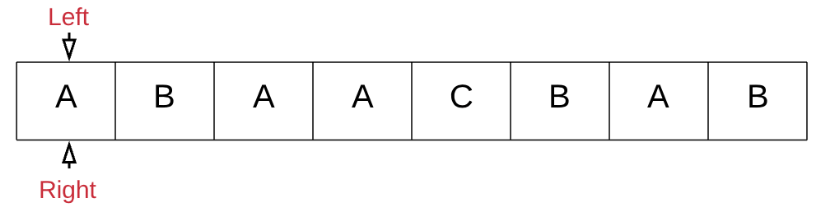
-
right向右移动扩展子串,直到子串包含T:
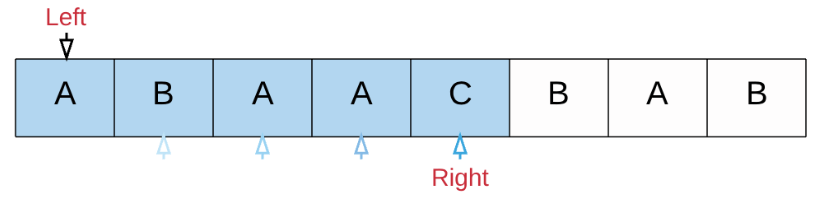
-
left向右移动收缩子串,直到最短满足T,记录子串:
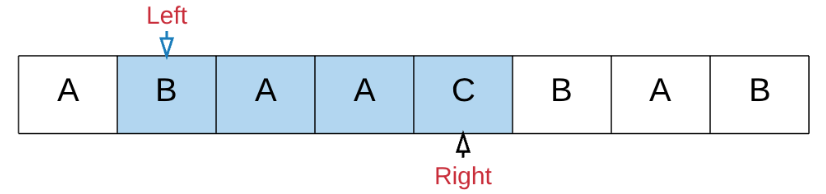
-
left再次右移,这时子串不再满足包含T:
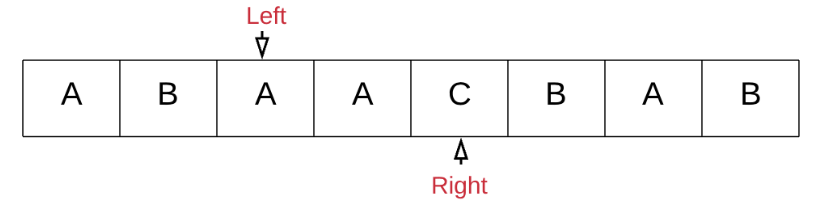
-
right从重复第二步骤,找到新的子串:
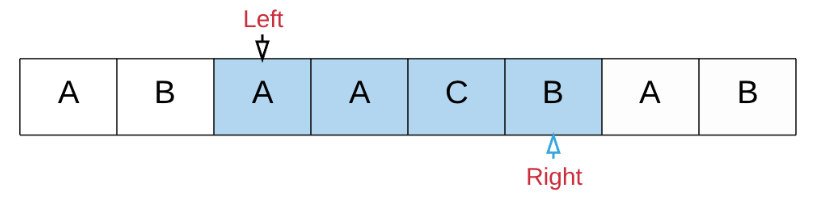
-
再次收缩子串,与之前的子串比较是否更短:
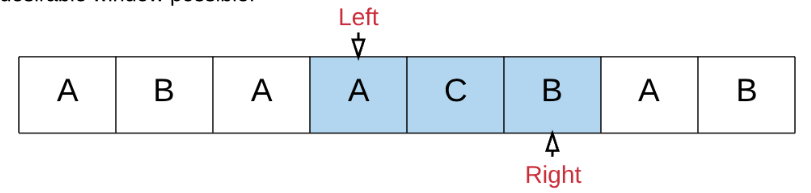
之前是使用map来做记录,需要26ms,后来第一名使用数组记录更快,可以跑进4ms。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
func minWindow(s string, t string) string {
m := make([]int, 128)
// 记录有多少个不同的字符
espect := 0
// 每次遇到一个字符就减一
// 在后面遍历的时候加一,遇到等于0表示当前字符恰好满足数量
for _, v := range []byte(t) {
if m[v] == 0 {
espect++
}
m[v]--
}
arrayS := []byte(s)
minStart, minLength := 0, math.MaxInt32
okCnt := 0
l, r := 0, 0
tightenLeft := func() {
// 收紧左边
for okCnt == espect {
v := arrayS[l]
l++
m[v]--
// 小于0表示当前字符是需求的字符,且数量已经不满足
if m[v] < 0 {
okCnt--
length := r - l + 2
if length < minLength {
minLength, minStart = length, l-1
}
break
}
}
}
// 向右扩展
for r < len(arrayS) {
v := arrayS[r]
m[v]++
// 等于0表示当前字符是需求的字符,且数量恰好满足
if 0 == m[v] {
okCnt++
tightenLeft()
}
r++
}
if minLength != math.MaxInt32 {
return string(arrayS[minStart : minStart+minLength])
}
return ""
}
|






